Excel。散布図をつくって近似曲線を表示したら、予測することができるのです。
<近似曲線と回帰分析>
折角のデータ。棒グラフや折れ線グラフで留めるのはもったいないですよね。
そこで、散布図をつくることで、データがどのように散布されているのか、さらに近似曲線をグラフに表示することで、予測もたてることができるかもしれません。
用意したデータです。
データがどのようにまとまっているのかを確認するために、散布図をつかってみましょう。
B7:C11を範囲選択します。
挿入タブの「散布図またはバブルチャートの挿入」にある「散布図」をクリックします。
散布図が表示されました。説明の都合上、グラフを大きく表示したいので、グラフタイトルは削除しております。
散布図に「近似曲線」の直線を描いていきます。
グラフ要素の追加ボタンにある「近似曲線」の「その他のオプション」をクリックします。
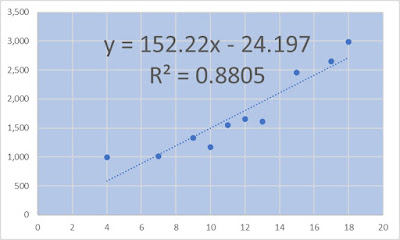
近似曲線の書式設定作業ウィンドウが表示されますので、「直線近似」を選択して、予測にある「グラフに数式を表示する」と「グラフにR-2乗値を表示する」にチェックします。
グラフに、近似曲線の直線近似と、数式が表示されました。
なお、見やすいようにプロットエリアを塗りつぶし、数式のフォントサイズもアップしています。
予測するには、この数式が必要になってきます。
R2乗の数値は何を意味しているのかというと、数式の精度を表していて、0~1の間の数値を表示しますが、「1」に近いほど、予測の精度は高いことを意味しています。
今回は、0.8805ということで、「1」に近いので、数式の精度は高いことを意味しています。
「y = 152.22x - 24.197」
この数式は、回帰式と呼ばれています。
y=ax-bという式で、「a」を「回帰係数」と呼び、「b」を「切片」と呼びます。
学生時代の一次方程式は、このために学んだのかもしれませんね。
横軸の「x」ですが、データをみると、来店数なので、例えば、来店数が「30」になった場合、売上高の予測値は、「y = 152.22×30 - 24.197」ですから、「4542.403」と算出された結果が予測されるとわかるわけですね。
このようなことから、データをしっかりそろえることで、いままで直感だったりした、予測よりも、数値として、ある程度予測した値を把握することが、比較的容易にできるようになります。