Excel。分析ツールの基本統計量を関数で算出してみよう。【Basic statistics】

Excel。分析ツールの基本統計量を関数で算出してみよう。

＜AVERAGE・STDEV.S・SQRT・COUNT・MEDIAN・MODE.SNGL・VAR.S・KURT・SKEW・MAX・MIN・SUM関数＞

アドインでデータ分析にある基本統計量をつかうことで、データのステータスを手早く確認することができます。

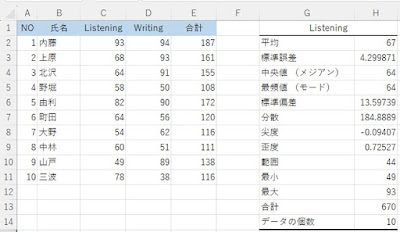
G列とH列に表示されているのが、C列のListeningの基本統計量です。

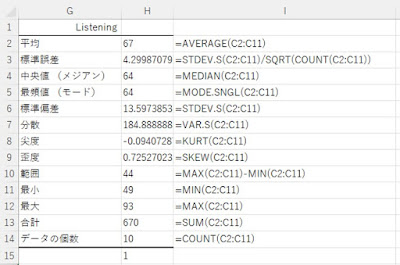
H列の基本統計量の値は、関数でも算出できるので、確認しておきましょう。

H2の平均は、AVERAGE関数です。

=AVERAGE(C2:C11)

標準誤差は、標準偏差をデータの件数の平方根で除算した値です。

=STDEV.S(C2:C11)/SQRT(COUNT(C2:C11))

で算出することができます。

STDEV.S関数は、「S」なので、数値をサンプルとした標準偏差を算出する関数です。

SQRT関数は、平方根を算出する関数です。

COUNT関数は、数値の件数を算出関数です。

中央値は、MEDIAN関数で算出できます。

=MEDIAN(C2:C11)

最頻値は、MODE.SNGL関数で算出できます。

最頻値は、データ内で一番多く登場した数値のことですね。

=MODE.SNGL(C2:C11)

標準偏差は、先程紹介した、STDEV.S関数で算出します。

=STDEV.S(C2:C11)

標準偏差は、データが平均値からどのぐらい外れているか（散っているのか）を表します。

分散は、VAR.S関数で算出します。

=VAR.S(C2:C11)

尖度（せんど）は、KURT関数で算出できます。

=KURT(C2:C11)

尖度は、正規分布を元に上下にどの程度偏っているかを表す値です。

歪度（わいど）は、SKEW関数で算出できます。

=SKEW(C2:C11)

歪度は、正規分布を元に左右にどの程度偏っているかを表す値です。

範囲は、最大値と最小値の範囲（レンジ）です。

最大値から最小値を減算すれば算出できます。

=MAX(C2:C11)-MIN(C2:C11)

最小は、MIN関数ですね。

=MIN(C2:C11)

最大は、MAX関数ですね。

=MAX(C2:C11)

合計は、SUM関数ですね。

=SUM(C2:C11)

最後は、データの個数なので、COUNT関数です。

=COUNT(C2:C11)

このように、基本統計量は様々な関数をつかって算出しています。

算出する項目が多いため、面倒なので、分析ツールをつかえるようならば、つかったほうが、楽なような気がします。

Excelの様々な関数の読み方や引数などを紹介。今回は、STDEV関数～STDEVPA関数です。【dictionary】

Excelの様々な関数の読み方や引数などを紹介。今回は、STDEV関数～STDEVPA関数です。

＜Excel関数辞典：VOL.75＞

今回は、STDEV関数～STDEVPA関数までをご紹介しております。

STDEV関数

読み方： スタンダードディブ　　

読み方： スタンダードディビエーション

分類： 互換性 

STDEV(数値1,[数値2],…)

数値群を標本データとみなした標準偏差を算出する　

STDEV.P関数

読み方： スタンダードディブ・ピー　　

読み方： スタンダードディビエーション・ピー

分類： 統計 

STDEV.P(数値1,[数値2],…)

数値群を母集団全体とみなした標準偏差を算出する

Pはポピュレーション

STDEV.S関数

読み方： スタンダードディブ・エス　　
読み方： スタンダードディビエーション・エス

分類： 統計 

STDEV.S(数値1,[数値2],…)

数値群を標本データとみなした標準偏差を算出する

Sはサンプル

STDEVA関数

読み方： スタンダードディブエー　

読み方： スタンダードディビエーションエー

分類： 統計 

STDEVA([値1,[値2],…)

全データを標本データとみなした標準偏差を算出する　

STDEVP関数

読み方： スタンダードディブピー　

読み方： スタンダードディビエーションピー

分類： 互換性 

STDEVP(数値1,[数値2],…)

数値群を母集団全体とみなした標準偏差を算出する　

STDEVPA関数

読み方：スタンダードディブピーエー

読み方：スタンダードディビエーションピーエー

分類： 統計 

STDEVPA([値1,[値2],…)

全データを母集団全体とみなした標準偏差を算出する

Excelの様々な関数の読み方や引数などを紹介。今回は、STDEV関数～STDEVPA関数です。【dictionary】

Excelの様々な関数の読み方や引数などを紹介。今回は、STDEV関数～STDEVPA関数です。

＜Excel関数辞典：VOL.75＞

今回は、STDEV関数～STDEVPA関数までをご紹介しております。

STDEV関数

読み方：スタンダードディブ　　

読み方：スタンダードディビエーション

分類： 互換性 

STDEV(数値1,[数値2],…)

数値群を標本データとみなした標準偏差を算出する　

STDEV.P関数

読み方： スタンダードディブ・ピー　　

読み方： スタンダードディビエーション・ピー

分類： 統計 

STDEV.P(数値1,[数値2],…)

数値群を母集団全体とみなした標準偏差を算出する　

Pはポピュレーション

STDEV.S関数

読み方： スタンダードディブ・エス　　

読み方： スタンダードディビエーション・エス

分類： 統計 

STDEV.S(数値1,[数値2],…)

数値群を標本データとみなした標準偏差を算出する　

Sはサンプル

STDEVA関数

読み方： スタンダードディブエー　　

読み方： スタンダードディビエーションエー

分類： 統計 

STDEVA([値1,[値2],…)

全データを標本データとみなした標準偏差を算出する　

STDEVP関数

読み方： スタンダードディブピー　　

読み方： スタンダードディビエーションピー

分類： 互換性 

STDEVP(数値1,[数値2],…)

数値群を母集団全体とみなした標準偏差を算出する　

STDEVPA関数

読み方： スタンダードディブピーエー　　

読み方： スタンダードディビエーションピーエー

分類： 統計 

STDEVPA([値1,[値2],…)

全データを母集団全体とみなした標準偏差を算出する　

Excel。標本データ数が少ない場合は、t分布（スチューデントのt分布）を利用します。【Student's "t "distribution】

Excel。標本データ数が少ない場合は、t分布（スチューデントのt分布）を利用します。

＜COUNT・AVERAGE・STDEV.S・T.INV.2T・SQRT関数＞

データがどのようになっているのか確認したくても、母集団の標準偏差がわからない。

さらに、サンプルデータの件数も少ない場合は、「t分布」を利用して推測することができます。

t分布は、スチューデントのt分布の略称ですね。

次のデータを使って必要な値を算出してみましょう。

 

最初は、標本数を算出します。

データ件数を算出しますので、COUNT関数をつかいます。

E2の数式は、

=COUNT(B2:B11)

算出結果は、10

標本平均ですが、これは、お馴染みAVERAGE関数で算出しますので、

E3の数式は、

=AVERAGE(B2:B11)

算出結果は、141.9

標本標準偏差を算出するには、STDEV.S関数で算出することができます。

今回は、サンプルデータが少ないことと、母集団の標準偏差がわからないため、STDEV.S関数を使います。

E4の数式は、

=STDEV.S(B2:B11)

関数自体は馴染みが薄いのですが、範囲選択を設定するだけで、簡単に算出することができます。

STDEV.S関数とSTDEV.P関数がありますが、SはSamle=標本の頭文字で、PはPopulation＝母集団を意味しています。

今回はサンプルデータの標本から算出させるので、STDEV.S関数をつかって算出させます。

算出結果は、34.13518875

 

これで、境界値である、t値を算出するための数値を算出することができました。

今回は、信頼度を95%とします。

自由度のE7は、

=E2-1

という数式を設定しています。

自由度は、独立して自由に選べる数値の数です。

t分布の場合は、標本数-1が自由度になります。算出結果は9ですね。

境界値（t値）を算出していきます。

t値も関数で簡単に算出することができます。

使う関数は、T.INV.2T関数です。

T.INV.2T関数は、t分布の両側の累積確率からt値を算出することができる関数です。

E8の数式は、

=T.INV.2T(1-E6,E7)

1-E6の引数である確率は、100%-95%で5%をつかいます。

算出された結果は、2.262157163

 

境界値（t値）まで算出できたので、上限信頼限界と下限信頼限界を算出しておきましょう。

上限信頼限界と下限信頼限界は、公式があります。

上限信頼限界は、

標本平均＋t値×標準偏差÷√標本数

下限信頼限界は、

標本平均－t値×標準偏差÷√標本数

この公式にのっとって、計算式を設定していきましょう。

なお、√（ルート）は、SQRT関数で算出することができます。

よって、上限信頼限界のE9には、

=$E$3+$E$8*$E$4/SQRT(E2)

オートフィルで数式をコピーして、下限信頼限界の計算式を作るため、絶対参照を使っています。

下限信頼限界のE10には、

=$E$3-$E$8*$E$4/SQRT(E3)

という計算式を設定します。

 

計算式から、上限信頼限界は、

166.318843

下限信頼限界は、

135.417629

と算出することができました。

このことから、母平均の区間指定結果は、信頼度95%とした場合。

135.417629≦μ≦166.318843

ということがわかりました。

なので、4/17の204は、外れすぎというところでしょうか。

このようなことが、関数をつかうことで、比較的簡単に算出することができます。

Excel。国語・英語・数学。標準化すれば、どこを強化すればいいか見えてきます。【STANDARDIZE関数】

Excel。国語・英語・数学。標準化すれば、どこを強化すればいいか見えてきます。

＜AVERAGE関数・STDEV.S関数・STANDARDIZE関数＞

会議の資料によくある、数字ばかりの資料。売上高や得点など実際の数値の方に目が向きやすい傾向があります。

単純にいえば、教科の得点など、数値が大きい方が、いいのに決まっていますから、そこに着目するわけですね。

例えば、次の教科ごとのテスト得点表があります。

国語と英語と数学のテスト結果の一覧ですが、これを見て、Aさんは数学を重点的に強化したほうがいい感じを受けますよね。

しかし、教科ごとによって、テスト内容は違いますし、難易度も変わりますよね。

これは、売り場ごとの商材によっても変わるのと同じですね。

このように条件が異なる場合では、平均と標準偏差を算出し、その後、平均と標準偏差を使って『標準化』した値を算出することで、状況が見えてきます。

では、平均と標準偏差を算出していきます。

お馴染みの平均ですが、B6の数式は、
=AVERAGE(B2:B5)
続いて標準偏差ですが、標準偏差を算出する関数は、STDEV.S関数です。

STDEV.S関数ダイアログボックスを表示してもいいですが、簡単なので、直接入力してもつくれます。

標準偏差を算出しているB7の数式は、
=STDEV.S(B2:B5)
数式自体はあっさりしていますが、これで標準偏差を算出することができます。

あとは、オートフィルで数式をコピーします。

この表だけではまだ『標準化』を算出したわけではありません。

今回は下側に同じフレームの表を用意します。

B10に標準化した結果を表示していきます。
標準化するための関数も用意されています。

それが、『STANDARDIZE関数』です。
平均と標準偏差を算出したのは、このSTANDARDIZE関数の引数で必要になるのも理由の一つです。

では、B10をクリックしてSTANDARDIZE関数ダイアログボックスを表示します。

Xには、B2を設定します。

平均には、B$6を設定します。

複合参照にしているのは、このあと、オートフィルで数式をコピーするからですね。
行番号を固定しておきます。

標準偏差には、B$7を設定します。平均と同じように、複合参照にしておきます。

あとは、オートフィルで数式をコピーします。

そして、平均と標準偏差も改めて算出しましょう。

これで、標準化を算出することができました。

標準正規分布グラフを思い出せばわかってきますが、0に近い方が平均に寄っているわけです。

要するに0から遠ざかると、平均値から外れる。

さらに、マイナスの場合は平均値以下ということなので、今回のような成績の場合、より注視されるのはマイナスの数値で、０より遠い数値ということになります。

例えばBさんの場合、英語が60点といい感じがしますが、国語の50点よりも、英語全体から見れば、よくないことがわかります。

なので、まずは英語をより注視して対応するほうがいいということが、見えてきたりします。

このように、数字の大小だけを判断材料にするのは、ちょっとどうなのかな？という時には、いろんな角度からみられる資料を作ってみるというのもいいのかもしれませんね。

Excel。事務職のデータ分析その8。標準化してみると見えてきます【Standardization】

Excel。事務職のデータ分析その8。標準化してみると見えてきます

＜標準化&STDEV.S関数&STANDARDIZE関数＞

最近は、事務職でも資料作りの一環で、
データ分析系の資料作成をする人が増えてきたそうですので、
あまり馴染みがないものも少しずつ慣れていくようにしましょう。

ということで、
店舗ごとに、どのジャンルに力を入れていけばいいのか？
改善するジャンルはどれ？
ということが見えてくる【標準化】について紹介します。

このような売上表があります。

数字だけ見ると、
【コーン菓子】を全店舗で力をいれて改善する必要があるようにみえますよね。

これは、数字の大小だけをみてしまうからですが、
それぞれ、単価が違うとか、売上個数が違うとかあるわけですね。

要するに、コーン菓子とアイスとケーキは、
別な条件で販売されているということを忘れてはいけません。

では、どうしたらいいのか？というと、
すべてある基準、すなわち統計学的に見やすくしてあげればいいわけです。

それが【標準化】です。

標準化を算出するには、
「平均」と「標準偏差」を算出する必要があります。

6行目に「平均」。
7行目に「標準偏差」を算出していきます。

B6には、=AVERAGE(B2:B5)という数式を設定します。
オートフィルでD6まで数式をコピーしましょう。

続いて、B7に「標準偏差」を算出しますので、
標準偏差を算出する関数である、
【STDEV.S関数】を使いますので、
STDEV.S関数ダイアログボックスを表示します。

数値1には、B2:B5を設定して、OKボタンをクリックします。

平均と同じように数式をコピーしましょう。

ここまで出来ました。

これらの数値を使って【標準化】を算出しますので、
A1:D7を範囲選択して、フレームだけ下方向にコピーします。

【標準化】を算出するには、
STANDARDIZE関数（スタンダーダイズ関数）
を使うと算出することが出来ます。

STANDARDIZE関数は、
平均と標準偏差をもとに値の変量を算出してくれる関数です。

なかなか、使う機会は少ない関数なので難しいように感じますが、
いたって簡単。

では、STANDARDIZE関数ダイアログボックスを
B11をクリックして表示しましょう。

Xには、B2を設定します。
平均には、B6を設定しますが、
このあとオーフィルで数式をコピーするので、
複合参照で行を止めておきますので、B$6

標準偏差には、B7でこちらも、複合参照にしますので、B$7

あとはOKボタンをクリックします。
出来た数式を、D14までコピーしましょう。

この値が、標準化された値です。
平均と標準偏差も先ほどと同様に算出してあげると、平均は0。

標準偏差は1と算出されます。
標準化では、
平均値を0・標準偏差を1としてデータを変換した値ということになります。

標準化する事によって、
例えば、新宿店では、ケーキの数値が悪いことがわかりますので、
改善をするのは、ケーキということがわかるのです。

売上金額だけを見ていたら、コーン菓子の数値が一番悪いので、
そこを改善対象にしていたはずですね。

このように【標準化】という方法があることを知っている、
また使った表を作成できるというのは、
今後、事務職であっても、知っておいたほうがいい事なのかもしれませんね。

Excel。事務職のデータ分析その5。標準偏差を関数で算出してみよう。【STDEV.S】

Excel。事務職のデータ分析その5。標準偏差を関数で算出してみよう。

＜STDEV.P関数とSTDEV.S関数＞

最近は、事務職でも資料作りの一環で、
データ分析系の資料作成をする人が増えてきたそうですので、
あまり馴染みがないものも少しずつ慣れていくようにしましょう。

ということで、
前回は、『標準偏差』の関数を使わないで算出してみましたので、
今回は、関数を使って、『標準偏差』を算出してみます。

まず、登場する関数は、
STDEV.P関数とSTDEV.S関数。

STDEV.P関数は、
スタンダード・ディビエーション・ポピュレーションと読みます。
データ全体の『標準偏差』を算出する関数です。

なお、Excel2007以前は、STDEVP関数なので、注意が必要です。
「.」（ドット）の有無の違いがあります。

もう一つの、STDEV.S関数は、
スタンダード・ディビエーション・サンプルと読みます。

データをサンプルと考え、そのデータから偏差の推定値を算出する関数です。
こちらの関数は、Excel2007以降に登場した関数です。

では、次の表があります。

H4をクリックして、STDEV.P関数ダイアログボックスを表示します。

数値1に、C3:C22を入力して、OKボタンをクリックします。

簡単に、『標準偏差』を算出することが出来ましたね。

なので、
前回、どういうプロセスで算出しているのかをご紹介したわけです。

でないと、どの数値を今後どのようにしていけばいいのかが、
わからなくなる危険性があるのです。

ではもう一つの、STDEV.S関数も算出してみましょう。

H5をクリックして、STDEV.S関数ダイアログボックスを表示しましょう。

数値1に、C3:C22を入力して、OKボタンをクリックします。

あとは、OKボタンをクリックしましょう。

算出されましたが、先ほどの、STDEV.P関数と算出結果が異なっていますよね。

これは、STDEV.P関数が、C3:C22の全データを使って算出しているのですが、
STDEV.S関数は、C3:C22のデータをサンプルとみて算出しています。

少し詳しく説明すると、
『分散』を求めるときに偏差の2乗の合計を算出して、
その値からサンプル数から-1（マイナス1）した値で除算して算出しています。

このため、算出された『標準偏差』の値は、
STDEV.P関数<STDEV.S関数となり、
STDEV.S関数の算出値のほうが大きくなります。

ただ、大きな差異がないので、
ビジネスの現場では、
どちらを使用してもかまわないといわれていますが…
数値がことなっているのですから、厳密には統計学上。違いはあるはずです。

さて、今回は、STDEV.P関数とSTDEV.S関数をご紹介しましたが、
『標準偏差』を短時間で算出できましたが、
分散を算出するために、平均から偏差を算出し、
偏差を2乗して、
その偏差の2乗の平均の平方根で『標準偏差』を求める方法も
知っていて損はないと思います。