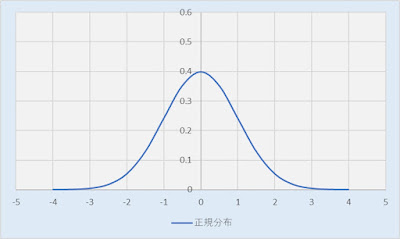
Excel。正規分布のグラフをつくって、尖度の変化もグラフならわかりやすい
<正規分布グラフ>
色々なグラフをExcelは作ることができますが、今回は、分析関係でお馴染みの『正規分布グラフ』をつくっていきます。グラフを作るには、データがなければ作ることができませんので、次のような表を用意しました。
正規分布グラフを作りますが、平均を「0」で標準偏差を「1」としたものを「標準正規分布」と呼ばれていますので、今回は、標準正規分布グラフを作っていきます。
4行目からの表は、グラフを作るためのデータです。
横軸のA列は、-4から4まで0.5ずつで作りました。
なお、細かくすると綺麗な正規分布グラフを作ることができます。
B列の正規分布は、『NORM.DIST関数』を使って算出します。
正規分布を英訳すると、Normal Distributionなので、わかりやすい関数ですね。
なお、B5の数式は、
=NORM.DIST($A5,B$1,B$2,FALSE)
NORM.DIST関数ダイアログボックスで確認してみましょう。
Xには、$A5
Xはグラフの横軸です。複合参照にしているのは、このあと、歪度・尖度のグラフを作るためです。
平均には、B$1
標準偏差には、B$2
関数形式には、FALSE
TRUEは、『累積分布関数』で算出しますが、今回は、『確率密度関数』なのでFALSEを使用します。
OKをクリックして、オートフィルで数式をコピーしたのが、現在の表のデータです。
それでは、グラフにしていきますので、A4:B21を範囲選択します。
挿入タブのグラフにある「散布図」から散布図(平滑線)を選択します。
今回は、グラフを大きく表示したいので、グラフタイトルは削除します。
また、グラフエリアとプロットエリアが白色だとわかりにくいので、着色しています。
確認ですが、尖度とは分布が平均値の近くに集中しているかどうかを確認することができます。
標準偏差が0に近くなれば当然、データのバラツキがすくないわけなので、平均の0に近づいたグラフになるはずです。
本当にそうなのかを確認するために表にデータを追加します。
平均と標準偏差を追加して、それに伴うように、グラフのデータを作りました。
先程B5のデータを算出した数式をオートフィルでコピーしました。
それで、グラフの範囲を修正しましょう。
カラーリファレンスで修正するのが便利ですね。
y2の曲線は、標準偏差の数値が大きいので、なだらかな曲線で表示されました。
y3の曲線は、標準偏差の数値が0に近いので、中心に寄った、尖った曲線で表示されています。
また、平均値の値が正数だと、右側に表示される(偏っている)ことがグラフでわかります。
標準正規分布グラフ及び、分布グラフは簡単に作れますので、機会があるときにつくってみると、色々わかりやすくなるかもしれませんね。